logic3

No．3速さの解説

まっすぐで平行な複線の鉄道を２つの列車ＡとＢがすれ違うように向かい合って一定の速さで進んでいます。列車Ｂの先頭がトンネルを出るとき、列車Ａの先頭がトンネルから３８００ｍ手前の踏み切りに来たので列車Ａの運転手さんが警笛を鳴らしました。列車Ｂの運転手さんは、列車の先頭がトンネルを出てから１０秒後に列車Ａの警笛を聞いて、すぐ自分も警笛を鳴らしたところ列車Ａの運転手さんは、自分が警笛を鳴らしてから１７．５秒後に列車Ｂの警笛が聞こえました。
列車ＡとＢの先頭どうしがすれ違うのは、トンネルの出口から何ｍのところですか。ただし、音の速さは秒速３５０ｍとします。

Ａ列車の警笛がＢ列車に聞こえたとき、音は

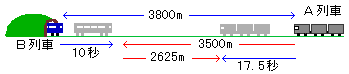
350×10=3500ｍ

動いていますから、Ｂ列車は10秒間に300ｍ動いています。だから、秒速は

(3800-3500)÷10=30m

であることがわかります。また、Ｂ列車の警笛がＡ列車に聞こえるのに 7.5秒かかっていますから、その間に音は

350×7.5=2625m

動いています。したがってＡ列車の秒速は

(3500-2675)÷17.5=50m

であることがわかります。
この２つの速さから、列車が出会うのは

3800÷(30+50)=47.5秒後

で、それはトンネルから

30×47.5=1425m

の地点です。