上りの電車が踏み切りを通過するとき、下りの貨物列車も近づいてきていて、踏み切りが 60秒間閉まるとき、この2つの列車は踏み切りから何mの地点で出会いますか。
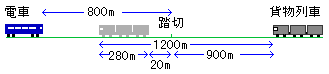
まず、電車が先に通過した場合は、電車が踏切から800mの地点にきたとき踏切が閉まります。 貨物列車は、それから60秒後に踏切を通過し終えますから、
20×60=1200m
手前にいることがわかります。詳しく表すと、下の図のように踏切の
1200-(280+20)=900m
手前にいることがわかります。このとき、離れている距離は
800+900=1700m
です。したがって、出会うまでの時間はとなり、貨物列車の動いた距離から踏切までの距離を求めましょう。
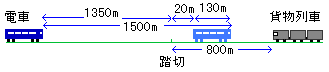
25×60=1500m
手前にいることがわかります。さらに、下の図のように表すと踏切の
1500-(130+20)=1350m
手前にいることがわかります。このとき、離れている距離は
800+1350=2150m
です。したがって、出会うまでの時間はと、踏切までの距離を求められます。